Я показываю, что по той же причине золотое сечение, $ phi = 1.6180334 .. $, можно считать самым иррациональным числом, что $ 1 + sqrt {2} $ можно считать вторым наиболее иррациональным числом, и действительно, почему $ (9+ sqrt {221}) / 10 $ можно считать третьим наиболее иррациональным числом.
Давайте представим игру между двумя детьми, Эмили и Сэмом — сильными и решительными по-своему, которые проводят всю свою жизнь, пытаясь перехитрить друг друга, вместо того, чтобы делать свою домашнюю работу. (Настоящая Генеративная Вражеская Сеть…)
Эмили гордо напоминает нам, что она одновременно носит то же имя, что и Эмили Дэвисон, самая известная из британских суфражисток; Эмили Балч, лауреат Нобелевской премии мира; Эмили дю Шатле, написавшая первый французский перевод и комментарий к «Принципам Исаака Ньютона »; Эмили Роблинг, главный инженер знаменитого нью-йоркского Бруклинского моста; Эмили Бронте, автор Wuthering Heights ; Эмили Уилсон, первая женщина-редактор New New Scientist ‘публикации; а также Эмми Нетер, которая произвела революцию в области теоретической физики.
С другой стороны у нас есть Сэм (и все его друзья миньоны, которых удачно называют Сэм-002, Сэм-003, Сэм-004), которые является частично человеком или частично роботом и играет в Minecraft или смотрит Youtube, 24/7.
Они соглашаются играть в игру, в которой Эмили думает о числе, а затем у Сэма (возможно, с помощью его миньонов) 60 секунд, чтобы найти дроби, равные числу Эмили.
Итак, игра начинается…
Эмили говорит « 8,5» .
Сэм и друзья быстро отвечают « 85/10 ″ ,…« 34/4 ″ ,… « 17/2 ″ ,…« 425/50 ″ ,…
Вскоре они понимают, что все эти ответы одинаково действительны, потому что все они e эквивалентные дроби. Будучи конкурентоспособными, они хотят выбрать единственного победителя, поэтому они все согласны с тем, что лучший ответ — тот, у которого наименьший знаменатель. И вот, 17/2 считается лучшим ответом.
На этот раз Эмили пытается усложнить задачу, выбрав ‘ 0.123456 ‘. После небольшой паузы Сэм хитро говорит: « 123456/1000000 ».
Эмили раздражает этот ответ. Она знает, что, хотя лучшим ответом была бы неприводимая дробь 1929/15625, Ответ Сэма все еще действителен, и, кроме того, он всегда сможет мгновенно ответить таким образом, если она выберет любое число с прекращение десятичного расширения .
На этот раз Эмили выбирает «$ pmb { pi} $».
На этот раз Сэм обернулся, чтобы разозлиться и утверждает, что это обманывает Они оба знают, что ответа нет, потому что $ pi $ — это иррациональное число и поэтому нет ни одной дроби, которая точно равна ему.
Поэтому они в конечном итоге соглашаются, что лучшим ответом будет та фраза, которая ближе к ее числу.
С этим новым правилом миньоны Сэма предлагают следующее: ' 3 ',… ' 31/10 ',…' 22/7 ',…' 16/5 ',…' 3927/1250 '.
Сэм смотрит на всех них снисходительно и немедленно выкрикивает « 3141592/1000000 »
Опять Эмили раздражается. Она понимает, что Сэм показал, что для любого иррационального числа вы можете (легко) выбрать дробь, которая будет произвольно близка к нему. То есть, рациональные числа всюду плотны.
Они оба знают, что дроби с маленькими знаменателями больше соответствуют духу игры, но Сэм говорит, что, поскольку его ответ был технически обоснованным, это ее ответственность (а не его ) придумать новое правило для улучшения вещей.
Эмили обдумывает способы оценки каждого ответа. Первоначально она думала, что для каждой фракции оценка может быть (абсолютной) разницей между ее числом и предложенной дробью, а затем умножаться на знаменатель. (Чем ниже, тем лучше).
Однако, поговорив с некоторыми из своих технических друзей, она решила сделать еще более строгим суровое наказание дробей с большими знаменателями. Такая система подсчета очков определенно заставит Сэма усердно работать, чтобы найти хорошие фракции. И, наконец, она предложила, чтобы для каждой фракции оценка была абсолютной разницей умноженной на квадрат знаменателя . Побеждает самый низкий балл.
Итак, для предыдущего значения $ pmb { pi} $ миньоны вычисляют свои баллы:
$$ 3 rightarrow 0.141, quad 31/10 rightarrow 4.1, quad 22/7 rightarrow 0,06, quad 16/5 rightarrow 1.5, quad 3927/1250 rightarrow 36 $$
В то время как Сэм идет последним с по-настоящему жалким и смущающим счетом $ 3141592/1000000 rightarrow 592 $.
Сэм теперь очень раздражен, он очень решительно настроен найти простой метод, который получит низкую оценку.
Позже на этой неделе, сидя за своим компьютером, у него была вспышка вдохновения.
Сначала он заметил, что $ pi = 3.14159… $.
Поэтому игнорирование дробной части этого подразумевало, что $ pi simeq 3 $.
Для лучшего приближения он отметил, что обратная величина предыдущей дробной части равна $ 1 / 0.14159265 = 7.0625133 $.
Итак, игнорируя дробную часть этого последнего числа, следует, что $ p i simeq 3 + cfrac {1} {7} = frac {22} {7} $.
Для еще лучшего приближения он отметил, что обратная величина предыдущей дробной части равна 1 / 0,0625133 $ = 15.996594… $
Опять же, игнорирование дробной части этого означает, что
$$ pi simeq 3 + cfrac {1} {7+ cfrac {1} {15} } = frac {333} {106} $$
Для еще лучшего приближения он отметил, что обратная дробная часть этого последнего числа составляет $ 1 / 0.996594 = 1,00341723 $.
Опять же, игнорирование дробной части этого означает, что
$$ pi simeq 3 + cfrac {1} {7+ cfrac {1} {15+ cfrac {1} {1}}} = frac {355} {113} $$
Далее он понял, что, поскольку числители каждой из дробей равны 1, и между различными числами всегда есть сложение, единственными важными числами являются те, которые спускаясь по диагонали. То есть 3, 7, 15 и 1. Таким образом, он разрабатывает краткий способ записи этих непрерывных дробей.
$$ pi simeq [3; 7,15,1] = frac {355} {113} $$
Он называет каждое из этих последовательных рациональных приближений «сходящимися», потому что он знает, что в предел они сходятся к $ pi $. Оценка для каждого из этих конвергентов:
$$ frac {3} {1} rightarrow 0.141, quad frac {22} {7} rightarrow 0.062, quad frac {333} {106} rightarrow 0.935, quad frac {355} {113} rightarrow 0.003, quad frac {103993} {33102} rightarrow 0.633 $$
Сэм снова очень счастлив, что он нашел систематический способ стабильно низких баллов. Затем он пишет компьютерную программу, чтобы быстро вычислить непрерывную дробь для любого заданного числа. Для $ pi $ это было:
$$ pi simeq [3; 7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,2,1,84,2,1,1,15,3,13,1,4,2,6,6,99,1,,…] $$
Хотя он не видел какого-либо существующего паттерна, он был удовлетворен тем, что (в принципе) он мог бы вычислить это до необходимого количества цифр.
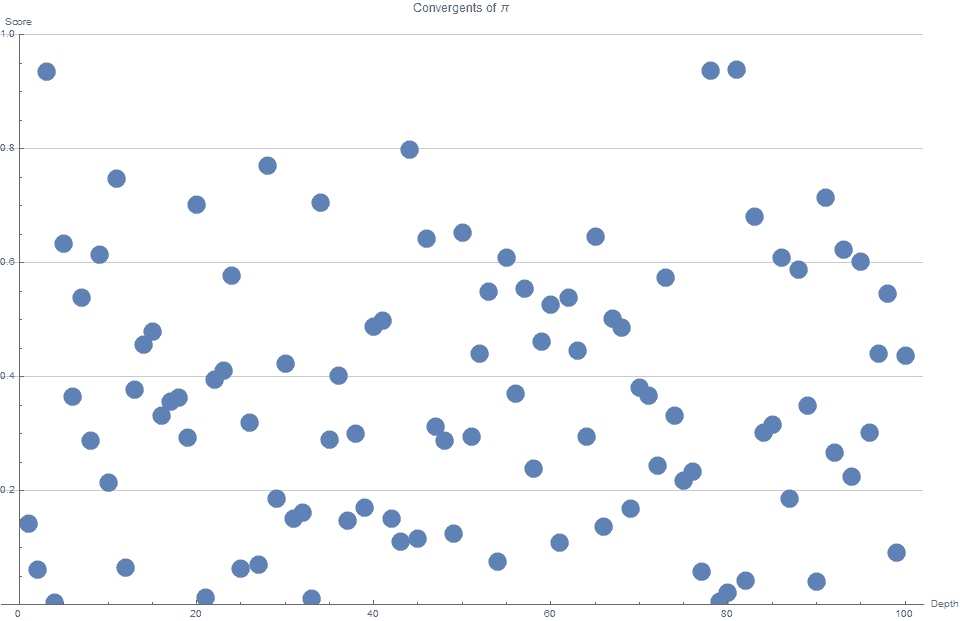
Затем его миньоны могут вычислять конвергенты, каждый из которых основывается на этой непрерывной дроби, на один уровень глубже, чем предыдущий. Когда они смотрят на оценки для первых 100 конвергентов (см. Рисунок 1), они замечают, что все оценки меньше 1. Это отличная новость, и она оказывается следствием теоремы Дирхлета, в которой говорится, что для любого иррационального числа существует бесконечное число непрерывных дробей, которые набирают меньше 1.
Они также заметили, что значения варьировались в широких пределах от 0 до 1 без различимой картины.
В течение следующих нескольких дней, зная, что Сэм использовал компьютер для вычисления своего ответы, Эмили всегда пыталась придумать действительно сложные цифры. К ним относятся:
$$ log pi, ; 2 ^ { pi}, ; е ^ 2, ; pi ^ e, ; sqrt [3] {2}, ; sin ( pi / 7),…. $$
Что они оба заметили, так это то, что для всех этих чисел распределение баллов по конвергентам было действительно похоже на приведенную выше диаграмму. То есть, оценки для конвергентов всегда варьировались довольно равномерно (но непредсказуемым образом) между 0 и 1.
Для Эмили, наиболее досадным следствием этого паттерна, было то, что множество конвергентов, которые миньоны посчитал, имел счет очень близко к нулю. Миньоны хвастались, что это означало, что если они продолжат свой процесс, то для всех чисел, которые выбрала Эмили, они смогут (теоретически) найти бесконечное число конвергентов, оценки которых были сколь угодно близки к нулю. Это очень раздражало ее.
Она действительно хотела найти число, которое было бы действительно трудно сопоставить с рациональными числами.
Однажды из-за явного раздражения Эмили не могла не думать о действительно сложное число, поэтому она просто выкрикнула: $ pmb { sqrt {7}} $.
Затем Сэм вычисляет непрерывную дробь следующим образом:
$$ sqrt {7} = [2; 1,1,1,4,1,1,1,4,1,1,1,4,1,1,1,4,…] = [2; overline{1,1,1,4}] $$
где подчеркивание указывает на то, что шаблон блока повторяется бесконечно.
По полной случайности Сэм и Эмили только что обнаружили свойство Лагранжа (1767) и Эйлера (1763) впервые обнаружили: а именно, что любая иррациональная квадратичная дробь будет иметь периодическую непрерывную дробь, и аналогично все периодические дробные дроби являются квадратичными иррациональными.
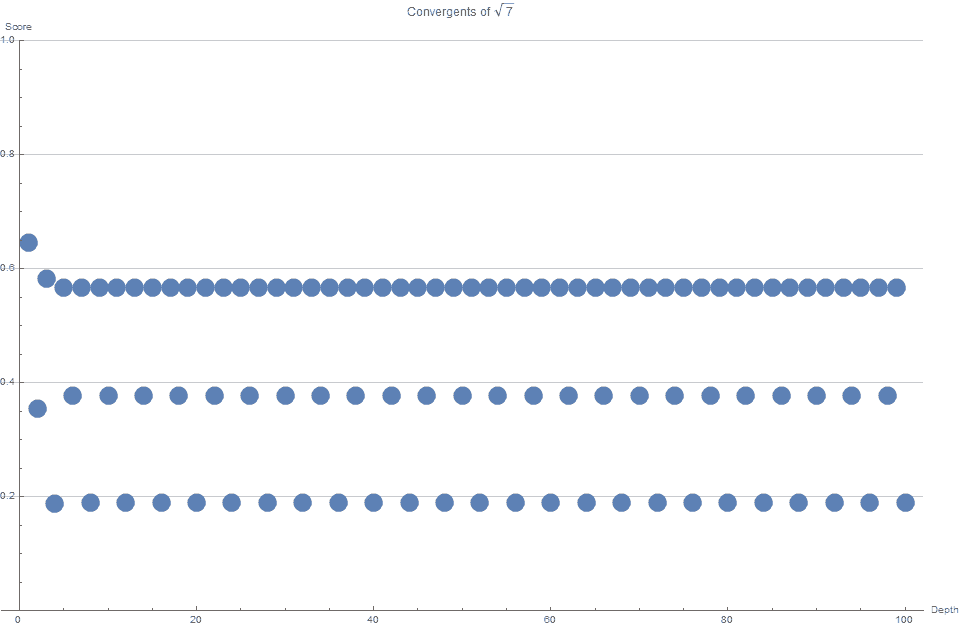
Но самый большой шок наступил, когда миньоны вычислили баллы для сходящиеся (см. рисунок 2). Баллы следовали невероятно четкой и регулярной схеме. Многие оценки сходились поочередно (чуть выше, потом чуть ниже, потом чуть выше, потом чуть ниже,…) вокруг критического порога, равного 0,188982, который, как они вскоре поняли, был равен $ 1 / sqrt {28} $.
Они оба знали, что это будет иметь некоторые глубокие последствия.
Сэм понял, что его миньоны могут найти бесконечное число сходящихся рациональных чисел, которые все (немного) меньше, чем $ 1 / sqrt {28} $. Но для любого другого меньшего показателя $ S $ (даже бесконечно меньшего, чем этот) Сэм и его миньоны смогут найти только конечное число дробей со счетом менее $ S $.
То есть, специальное значение $ 1 / sqrt {28} $ представляет собой критический порог между бесконечным числом решений и только конечным числом решений.
Миньоны больше не могут похвастаться тем, что они могут найти бесконечное число дробей со счетами, произвольно близкими к нулю! Эмили нашла число, где нижний предел баллов не был равен нулю. Наконец она нашла
плохо аппроксимируемое число (понятие, тесно связанное с последовательностями с низким расхождением), и она была в восторге.
I
Эмили наткнулась на очень нелогичный образец, впервые обнаруженный Маркоффом (в этой очень специфической области математики его имя традиционно пишется как «Маркофф», но во всех других областях оно обычно пишется 'Марки'). Он обнаружил, что из всех возможных чисел те, которые являются иррациональными корнями квадратного уравнения, сложнее аппроксимировать, чем все другие иррациональные числа.
Кроме того, исследовав, она обнаружила одну из самых глубоких теорем в области числа. Теория, а именно теорема Туэ-Рота-Зигеля, из которой вытекает следствие, что числа, являющиеся корнями полинома (алгебраические числа), сложнее приблизить, чем трансцендентные числа, такие как $ e $ или $ pi $.
То есть, несмотря на ее интуицию, числа вида $ a + b sqrt {c} $ для рациональных чисел $ a, b, c $ на самом деле намного сложнее приблизить числа, чем числа типа $ e $ или $ pi $!
Эмили продолжила свое исследование квадратичных иррациональных чисел и вскоре узнала, что всякий раз, когда она выбирает число, являющееся иррациональным корнем квадратного уравнения $ ax ^ 2 + bx + c = 0 $ для целых чисел $ a, b , c $, критический нижний порог будет включать (если не будет совпадать) с выражением $ 1 / sqrt {b ^ 2-4ac} $.
Это помогло объяснить, почему в исходном примере, который соответствовал квадратному уравнению $ x ^ 2-7 = 0 $, критическое значение было равно $ 1 / sqrt {28} $. Вскоре она поняла, что может использовать эту модель, чтобы найти квадратное уравнение, где значение дискриминанта, $ b ^ 2-4ac $, было как можно меньше. Это заставит Сэма получить действительно высокий (и, следовательно, плохой) результат. Дискриминант не может быть 1 или 4, так как это не приведет к иррациональному корню. Затем, используя логику четности, она поняла, что квадратик с целыми коэффициентами не может иметь дискриминант 2 или 3. Таким образом, ей нужно было найти тот, где дискриминант был равен 5.
Она вскоре было найдено самое удивительное квадратное уравнение: $ x ^ 2-x-1 = 0 $.
Положительный корень этого квадратного уравнения был $ x = (1+ sqrt {5}) / 2 $, которую она определила как Золотое сечение, $ phi $.
Исходя из вышеизложенного, она предсказала, что это значение $ x $ приведет к критическому порогу $ 1 sqrt {5} simeq 0.4472 $. , которая была теорема Гурвица.
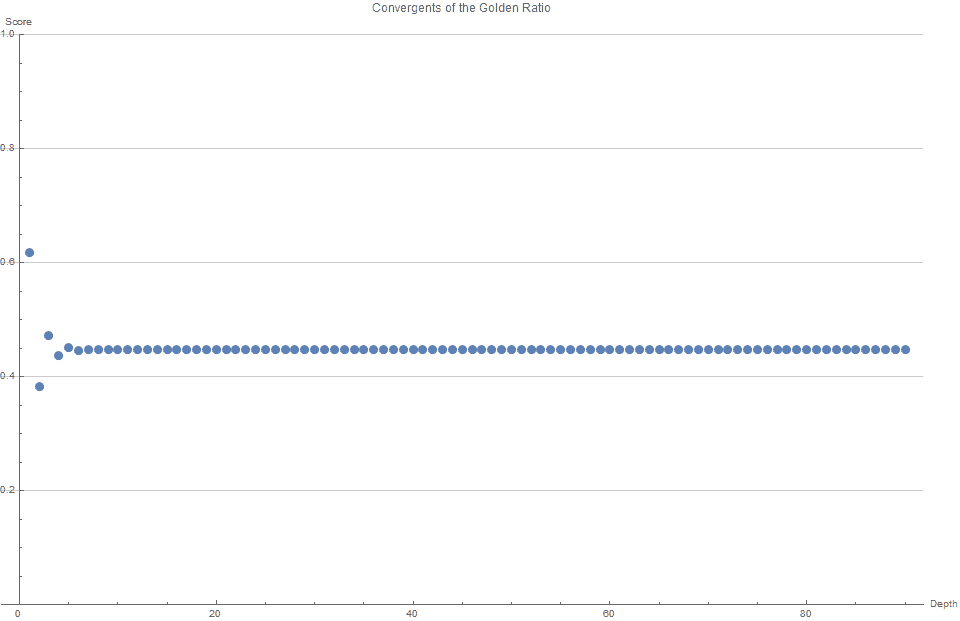
Сэм обнаружил, что непрерывная дробь для этого значения была очень элегантной, и его миньоны подтвердили (рисунок 3), что действительно критическая оценка была равна $ 1 / sqrt {5} $.
$$ phi = (1+ sqrt {5}) / 2 = [1;1,1,1,1,1,1,1,1,…] = [1; overline{1}] simeq 1.618033 $$
Эмили была в полном восторге, потому что теперь она нашла окончательное число, которое заставило Сэма иметь самое высокое (худшее (худшее) ) критический пороговый показатель.
И хотя многие знали, что золотое сечение является наиболее эстетичным аспектным соотношением для прямоугольников, где греческий Парфенон является постером ребенка для этого утверждения (см. рисунок 4), теперь она имела более глубокое понимание его значения.
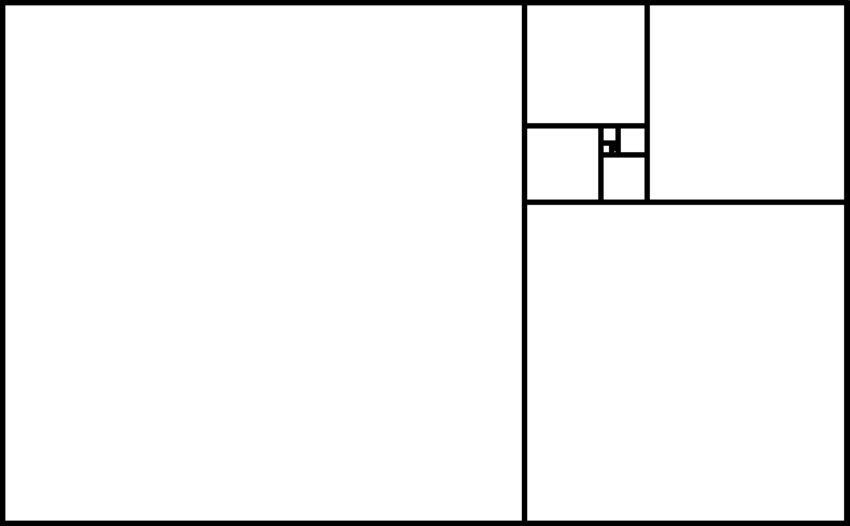
Она также узнала кое-что, что многие люди не осознали. А именно, золотое сечение является самым иррациональным числом, а не (напрямую), потому что его непрерывная доля состоит только из единиц; но скорее потому, что его критическая оценка — которая отделяет мир бесконечных рациональных чисел от конечного числа рациональных — была самой большой возможной критической оценкой.
Не довольствуясь почтением к лаврам, в ближайшие дни она обнаружила, что целый ряд квадратных уравнений, дискриминант которых равен 5, и, следовательно, также имеет критический пороговый балл $ 1 / sqrt {5} $. Вот некоторые из них, а также их непрерывные дроби.
begin {align}
x ^ 2-x-1 = 0 & rightarrow x = (1+ sqrt {5}) / 2 & = [1;1,1,1,1,1,1,1,1,…] & = [1; overline{1}] & = 1.618033 \ nonumber
x ^ 2 + x-1 = 0 & rightarrow x = (- 1+ sqrt {5}) / 2 & = [0;1,1,1,1,1,1,1,1,…] & = [0; overline{1}] & = 0.618033 \ nonumber
x ^ 2-3x + 1 = 0 & rightarrow x = (3+ sqrt {5}) / 2 & = [2;1,1,1,1,1,1,1,1,…] & = [2; overline{1}] & = 2.618033 \ nonumber
x ^ 2-5x + 5 = 0 & rightarrow x = (5+ sqrt {5}) / 2 & = [3;1,1,1,1,1,1,1,1,…] & = [3; overline{1}] & = 2.618033 \ nonumber
…
end {align}
Она узнала, что если $ x $ было оптимальным числом (например, $ phi $), то для любых целых чисел $ a, b , c, d $ такое, что $ ad-bc = pm 1 $ (целочисленное преобразование Мёбиуса), тогда $ frac {ax + b} {cx + d} $ также будет равно оптимальным числом. Итак, вот еще немного:
$$ frac {1} { phi + 3} simeq 0.216542 = [0; 4,1,1,1,1,1,1,1,ldots] $$
$$ frac { phi + 1} {2 phi + 1} simeq 0.619034 = [0; 1,1,1,1,1,1,1,1,ldots] $$
$$ frac { phi + 2} { phi + 3} simeq 0.783458 = [0; 1,3,1,1,1,1,1,1,ldots] $$
$$ frac {3 phi-2} {2 phi-1} simeq 1.276390 = [1; 3,1,1,1,1,1,1,1,ldots] $$
То есть она нашла метод для построения бесконечного числа значения $ x $, которые были эквивалентны $ phi $ и, следовательно, одинаково иррациональны, как $ phi $. И для каждого из этих чисел их непрерывная доля отличалась в начале, но в конечном итоге стала идентичной повторяющемуся блоку $ phi $. (Теорема Серрата).
Сэм быстро устал играть в эту игру, зная, что критический счет всегда будет $ 1 / sqrt {5} $, поэтому он заставил Эмили изменить правила игры. Таким образом, он применил правило: она больше не могла произносить число, эквивалентное $ phi $, золотому сечению.
Эмили была очень разочарована, потому что она очень полюбила $ phi $. и все его удивительные свойства, но в конце концов она смягчилась и согласилась на изменение правила.
Затем Эмили начала поиск более специальных значений $ a, b, c $, так что соответствующий квадратичный иррациональный будет действительно трудно приблизиться. Вскоре она определила квадратное уравнение
$$ x ^ 2-2x-1 = 0 rightarrow x = 1 + sqrt {2} = [2;2,2,2,2,…] = [2;overline{2}] $$
Она предсказала, что это будет иметь критическую оценку $ 1 / sqrt {8} simeq 0.353553 $, однако она не была уверена, что это лучшее, что она могла сделать. Поэтому она пошла в свою местную библиотеку и обнаружила, что Маркофф в возрасте 24 лет защитил кандидатскую диссертацию на эту тему. В своей диссертации он классно установил явное взаимно однозначное соответствие между каждым классом эквивалентности иррациональных чисел и отсортированными марковскими триплетами. Сортированные марковские триплеты были такими положительными целыми числами $ 0 <m_1 leq m_2 leq m $, что:
$$ m ^ 2 + m_1 ^ 2 + m_2 ^ 2 = 3m m_1 m_2 $$
Кроме того, он показал, что все триплеты Маркова могут быть построены через дерево Маркова (см. Также числа Маркова). Это дерево обладает множеством элегантных геометрических свойств (см. Также здесь.)
Последовательность целых чисел $ m $, удовлетворяющих этому уравнению:
$$ 1,2,5,13,29,34 , 9,169,194,223,433,610,… $$
Затем для каждого члена этой последовательности он определил новую последовательность (спектр Маркова-Лагранжа). Эти новые значения соответствовали оценкам для каждого из последовательных классов квадратичных иррациональных чисел.
$$ mu_m = frac { sqrt {9m ^ 2-4}} {m} = { sqrt {5}, sqrt {8}, frac { sqrt {221}} {5}, frac { sqrt {1517}} {13},… } $$
Как и ожидалось, первый член соответствует квадратному уравнению $ x ^ 2-x-1 = 0 $ и квадратному иррациональному $ x = (1+ sqrt {5}) / 2 $.
И во многом к удовлетворению Эмили второе слагаемое в последовательности соответствовало квадратному уравнению $ x ^ 2 + 2x-1 $ и квадратичному иррациональному $ x = 1 + sqrt {2} $, которое было тем же, которое она догадалась. Это было доказательством, которое она искала.
Сэм подсчитал, что постоянная дробь для этого значения.
$$ 1+ sqrt {2} = [2;2,2,2,2,2,2,…] = [2; overline{2}] = 2.414213562… $$
И его миньоны подтвердили, что критическая оценка для этого числа действительно была $ 1 / sqrt {8} $.
Сэм и Эмили также подтвердили, что $ sqrt {2 } $ было эквивалентно $ 1 + sqrt {2} $, и поэтому также имело критическую оценку $ 1 / sqrt {8} $.
Следовательно, второе наиболее нерациональное число равно $ 1 + sqrt {2} $.
$$ sqrt {2} = [1;2,2,2,2,2,…] = [1; overline{2}] simeq 1.41421356 $$
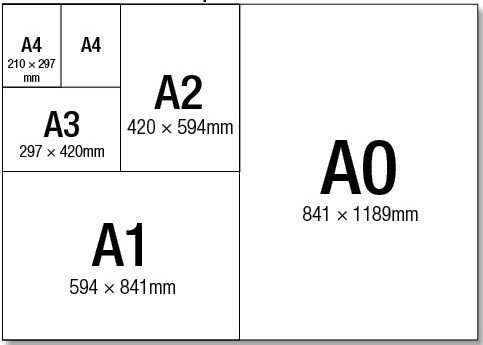
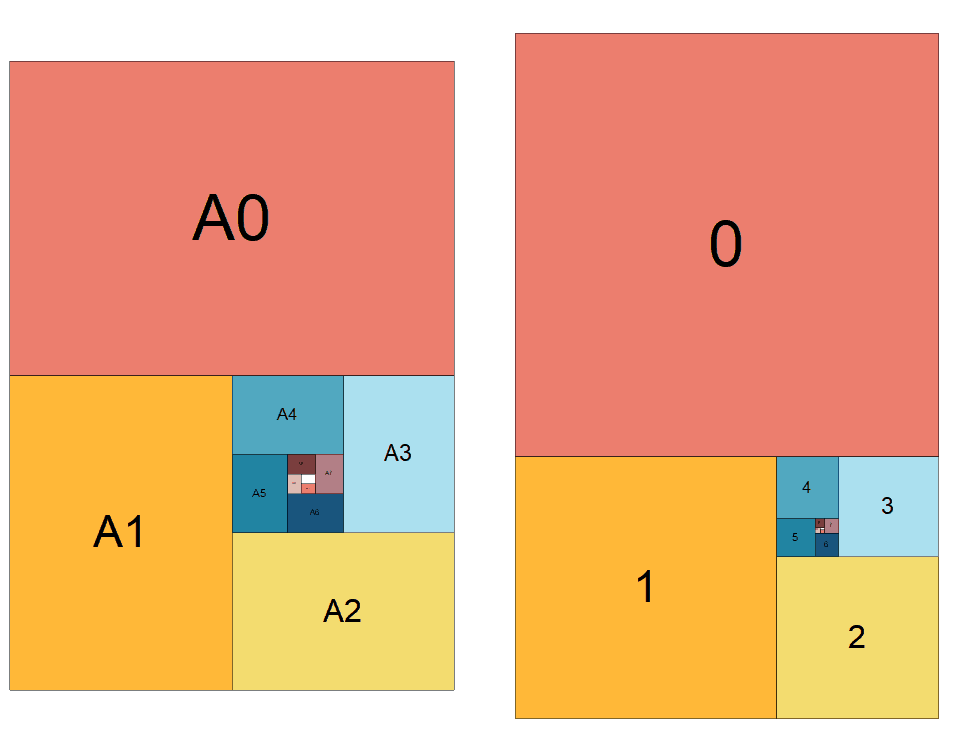
Учитывая новую найденную особую природу $ sqrt {2} $, Эмили задалась вопросом, есть ли был прямоугольник с такими же элегантными свойствами, как золотой прямоугольник. Оказалось, что был один. И не только это, но он был применен к одному из самых распространенных предметов домашнего обихода (см. Рисунок 5! Серия бумаги A ISO определена с точки зрения соотношения сторон $ sqrt {2} $. Каждый размер бумаги точно половина площади предыдущего, с $ A0 $ площадью ровно один квадратный метр.
Для Сэма вычислили, что $ frac {297} {210} = frac {594} {420} = [1;2,2,2,2,2] $ and that $ frac {1189} {841} = [1;2,2,2,2] $.
[1 9459024]
На этот раз Сэму не понадобилось много времени, чтобы вызвать другое новое правило: Эмили не могла сказать ни одного числа, эквивалентного $ phi = (1+ sqrt {5}) / 2 $ или $ 1 + sqrt {2} $.
Поэтому, согласившись, Эмили глубоко вздохнула и попробовала следующий номер в серии Маркова: $ frac { sqrt {221}} {8} $. Это выглядело намного страшнее, чем два предыдущих термина, но она верила …
Она нашла соответствующую квадратичную функцию, $ 5x ^ 2-9x-7 $, и ее квадратическую иррациональную $ x = (9 + sqrt {221}) / 10 $.
Она не была уверена, какой будет продолжающаяся дробь. Сэм вычислил длительную долю следующим образом:
$$ x = (9+ sqrt {221}) / 10 = [2;2,1,1,2,2,1,1,2,2,1,1,2,…] = [2;overline{2,1,1,2}] simeq 2.38660687 $$
И его Миньоны действительно подсчитали, что критическая оценка была $ frac {5} { sqrt {221}} $, которая была обратной величиной 3-го марковского члена.
Следовательно, третье наиболее нерациональное число — $ (9+ sqrt {221}) / 10 $.
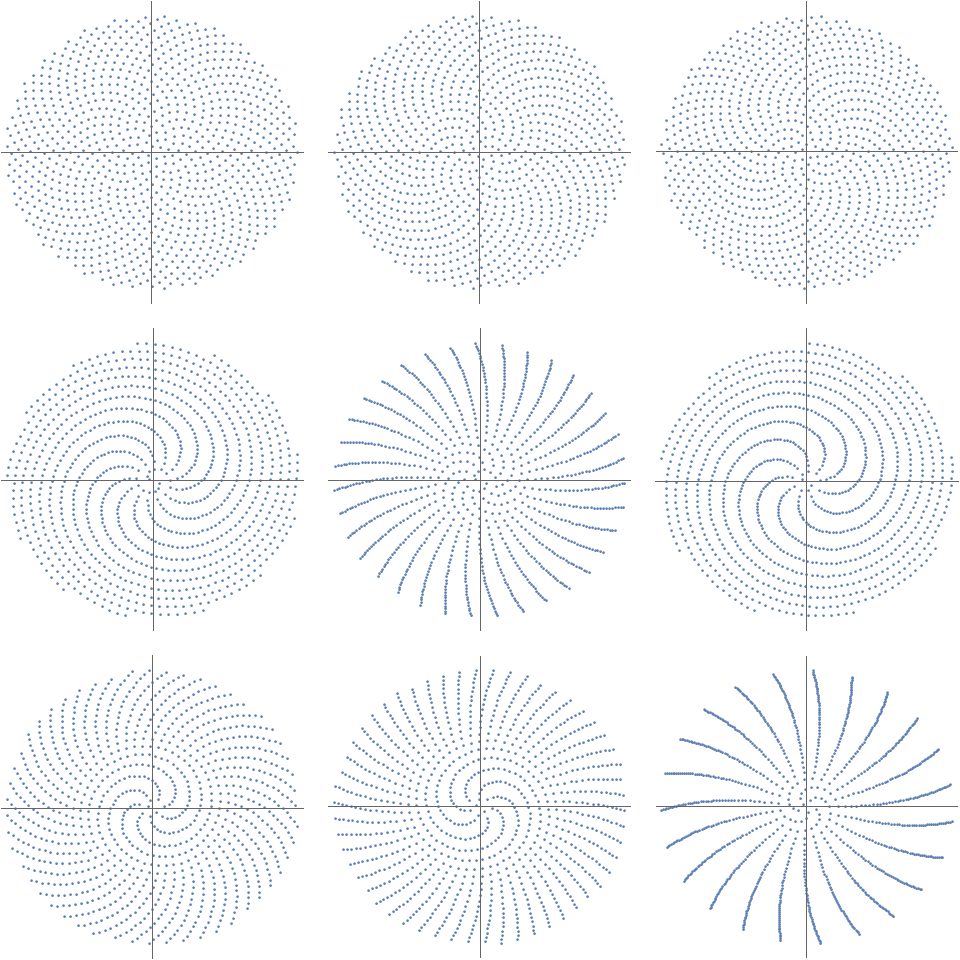
Хотя я не знаю ни одного эквивалентного прямоугольника, который бы использовал элегантность $ (9+ sqrt {221}) / 10 $ (или любого из его эквивалентов), для этих визуально наклонных фигур 6 показывает логарифмическую спираль, определенную в соответствии с полярным уравнением;
$$ (r, theta) = ( frac { sqrt {k}} {n}, frac {2 pi k} { г}); quad textrm {for} 1 leq k leq n = 1000. $$
Различные значения $ z $ создают разные спирали. Лучшие три основаны на трех специальных иррациональных числах: $ z = (1+ sqrt {5}) / 2; z = 1+ sqrt {2} $ и $ (9+ sqrt {221}) / 10 $, в то время как остальные шесть являются случайными значениями, показанными для сравнения. Ключевым моментом является то, что чем ближе значение $ z $ к рациональному числу, тем более заметными будут спиральные плечи с псевдонимами.
***
К концу этой игры Эмили и Сэм узнали, что золотое сечение, $ phi = (1+ sqrt {5}) / 2 $, действительно было самым иррациональным числом. То есть это было самое трудное число, чтобы приблизиться с дробью. Это было хорошее следствие, что непрерывная дробь для этого $ phi $ была просто $ [1;1,1,1,1,ldots] $, и что точки в золотой спирали были очень равномерно распределены.
Они также узнали, что были ( бесконечно) много других чисел, которые были одинаково иррациональны. Она могла найти их, используя целочисленное преобразование Мёбиуса или найдя эквивалентные непрерывные дроби.
Реальный приз в этой игре, однако, заключался в том, что они могли, наконец, ответить на вопрос « Так что, если золотое сечение является наиболее иррациональным числом, то какое второе и третье наиболее иррациональное число? «
Второе наиболее иррациональное число было $ 1 + sqrt {2} $, чья непрерывная дробь была $ [2;2,2,2,2,ldots] $. Хотя они, вероятно, не смогли бы догадаться об этом факте, элегантность этого числа означала, что они не были слишком удивлены этим результатом.
Однако, без сомнения, самым удивительным открытием из игры было то, что третье наиболее иррациональное число было самым непритязательным из чисел: $ (9+ sqrt {221}) / 10 $, чья непрерывная дробь $ [2;1,1,2,2,1,1,2,2,1,1,ldots] $, была простой, но не вполне очевидной.
Каким-то образом, хотя и завоевав место на подиуме, это специальное число утонуло в забвении , теперь без ведома для всех, кроме очень маленького меньшинства. Более того, более поздние работы Маркова о цепях Маркова затмили его основополагающую работу в теории диофантовых приближений.
Итак, на следующей званой вечеринке, когда вы устали говорить о погоде, почему бы не рассказать им об Андрее Маркове и о том, как он доказал, что тогда число $ (9+ sqrt {221}) / 10 $ было третьим самым иррациональным числом?
Не все персонажи и события, изображенные в этой статье, являются полностью вымышленный. Любое сходство с реальными событиями или людьми, живыми или мертвыми, в том числе с двумя моими детьми в реале Сэмом и Эмили, вероятно, верно ».
Меня зовут Мартин Робертс. У меня есть докторская степень в теоретической физике. Я люблю математику и вычисления. Я открыт для новых возможностей — консалтинга, контракта или полного рабочего дня — так что давайте поговорим о том, как мы можем работать вместе!
Заходите, следуйте за мной в Twitter: @TechSparx!
Мои другие контактные данные можно найти здесь.
] Другие сообщения, которые вам могут понравиться:








